ShortestPath

Description

This operation produces an FST containing the n -shortest paths in the input FST. The n -shortest paths are the n -lowest weight paths w.r.t. the natural semiring order. The single path that can be read from the ith of at most n transitions leaving the initial state of the resulting FST is the ith shortest path.

The weights need to be right distributive and have the path property. They also need to be left distributive as well for n -shortest with n > 1 (valid for TropicalWeight).

Usage

template<class Arc>
void ShortestPath(const Fst<Arc> &ifst, MutableFst<Arc> *ofst, size_t n = 1);

fstshortestpath [--opts] a.fst out.fst
    --nshortest: type = int64, default = 1
      Return N-shortest paths
    --unique: default = false
      Return only distinct strings (NB: must be acceptor; epsilons treated as regular symbols)

Examples

A:

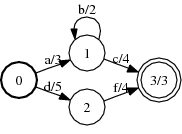(TropicalWeight)

Shortest path in A:

2-shortest paths in A:

Complexity

ShortestPath:

• 1-shortest path:
  • Time: O(V log V + E)
  • Space: O(V)
• n-shortest paths:
  • Time: O(V log V + n V + n E)
  • Space: O(n V)

Caveats

See here for a discussion on efficient usage.

See Also

ShortestDistance, State Queues

References

• Mehryar Mohri. Semiring Framework and Algorithms for Shortest-Distance Problems, Journal of Automata, Languages and Combinatorics, 7(3):321-350, 2002.
• Mehryar Mohri and Michael Riley. An Efficient Algorithm for the n-best-strings problem, In Proceedings of the International Conference on Spoken Language Processing 2002 (ICSLP '02).

-- CyrilAllauzen - 05 Jul 2007