Minimize

Description

This operation performs the minimization of deterministic weighted automata and transducers.

If the input FST A is an automaton (acceptor), this operation produces the minimal automaton B equivalent to A, i.e. the automata with a minimal number of states that is equivalent to A.

If the input FST A is a transducer, this operation internally builds an equivalent transducer with a minimal number of states. However, this minimality is obtained by allowing transition having strings of symbols as output labels, this known in the litterature as a real-time transducer. Such transducers are not directly supported by the library. By defaut, Minimize will convert such transducer by expanding each string-labeled transition into a sequence of transitions. This will results in the creation of new states, hence losing the minimality property. If a second output argument is given to Minimize, then the first output B will be the minimal real-time transducer with each strings that is the output label of a transition being mapped to a new output symbol, the second output transducer C represents the mapping between new output labels and old output labels. Hence, we will have that A is equivalent to B o C.

Usage

template<class Arc>
void Minimize(MutableFst<Arc> *fst, MutableFst<Arc> *sfst = nullptr, float delta = kDelta, bool allow_nondet = false);

fstminimize  in.fst [out1.fst [out2.fst]]

Examples

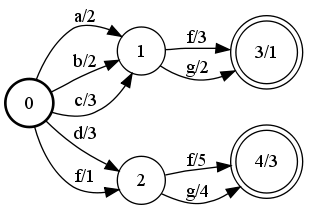
Acceptor minimization

A	B

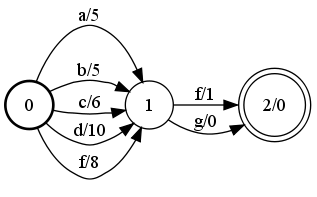Minimize(A, &B);
fstminimize a.fst b.fst

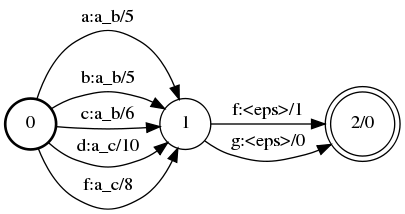
Transducer minimization

A	B

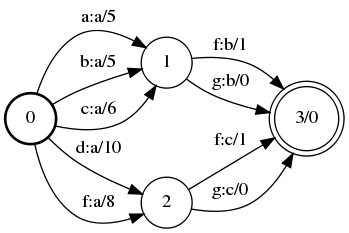Minimize(A, &B);
fstminimize a.fst b.fst

A	B	C

Minimize(A, &B, &C);
fstminimize a.fst b.fst c.fst

Complexity

Minimize

• Time:
  • Acyclic: O(E)
  • Unweighted: O(E log V)
  • Weighted: complexity of shortest distance + complexity of unweighted minimization

References

• John E. Hopcroft. An n log n algorithm for minimizing the states in a finite automaton. In Z. Kohavi, editor, The Theory of Machines and Computations, pages 189-196. Academic Press, 1971.
• Mehryar Mohri. Minimization algorithms for sequential transducers. Theoretical Computer Science, 234(1-2): 177-201, 2000.
• Dominique Revuz. Minimisation of Acyclic Deterministic Automata in Linear Time. Theoretical Computer Science, 92(1): 181-189, 1992.